20220513

一红黑树的原理

在理解红黑树的原理之上，建议先学习二叉树，可以对AVL树做简单了解。
红黑树(Red-black tree)是一种自平衡的二叉查找树，是一种数据结构，典型的用途是实现关联数组。红黑树的结构复杂，但它的操作有着良好的最坏情况运行时间，它可以在O(logN)时间内完成查找、插入和删除，N是树中元素的数量。

1.1 红黑树定义

红黑树中每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色，在二叉树的要求以外，增加了如下额外的要求：

节点是红色或黑色
根是黑色的
所有叶子节点都是黑色，这里的叶子节点是NIL(null)节点
每个红色节点必须有两个黑色的子节点，或者说每个叶子节点到根的所有路径上不能有两个连续的红色节点
从任一节点到其每个叶子的所有简单路径都包含相同数量的黑色节点（即黑高度相同）

上述的定义要完全掌握，这样在后面才能实现红黑树。红黑树是内存敏感型的树状数据结构，与B树或B+树不同，红黑树对磁盘的敏感性不高。如下图所示，就是一棵红黑树：
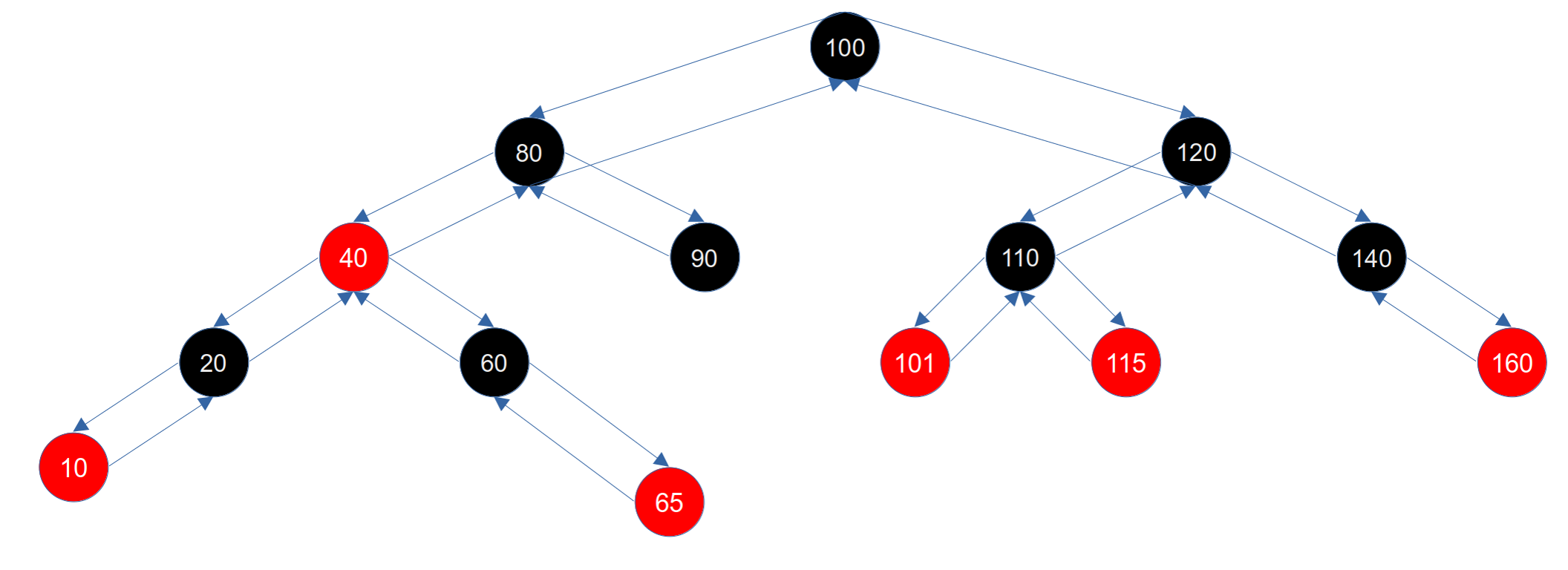
RedBlackTree-1.1-1
上图中未展示叶子节点（NIL节点是黑色的），下面的代码示例我们也会以这张图为基础来展开。
上图的红黑树插入顺序是：120、140、100、160、80、110、101、115、60、90、40、20、10、65

1.2 红黑树的优点

红黑树和AVL树一样都对插入时间、删除时间和查找时间提供了最好可能的最坏情况担保，在计算机几何中使用的很多数据结构都可以基于红黑树实现；在函数式编程中也特别有用，例如关联式数组和集合，每次插入、删除之后它们能保持为以前的版本。

1.3 红黑树的应用

红黑树作为很多场景的底层数据结构，应用场景也很广：

epoll的实现，内核会在内存开辟一个空间存放epoll的红黑树，并将每个epollfd加入到红黑树中，一般epoll会设置LT水平触发，当网卡有数据到来，可读缓冲区不为空就会一直触发EPOLLIN事件，而之前注册了对EPOLLIN事件感兴趣的socketfd就会有专门的队列存储，内核会遍历队列搜寻对应的socketfd,因为红黑树查找有近似O(logN)的时间复杂度，所以10亿个socket也只需要查找近20次，效率很高
进程调度，内核CFS队列，以红黑树的形式存储进程信息
Java（1.8）中的HashMap、ConcurrentHashMap当出现哈希冲突后链表超过指定长度就会转变为红黑树的形式来组织
内存池的内存管理，比如空闲链表freelist可以通过红黑树来组织，这样malloc的时候要找到符合大小的内存块，比链表的结构效率更高。

二红黑树的实现

下面我们以C++语言实现红黑树，以最简单的int作为value（key），可自行变更为模板。

2.1 红黑树代码框架

首先有一个链式的节点，这个节点存储了数据以及左子、右子、父节点的指针，并且有标识节点的颜色的能力；其次有对外的接口，添加、删除、查找等能力的树对象。

2.1.1 节点设计

TreeNode设计如下：

class TreeNode {
private:
    /** 父节点 */
    TreeNode *parent{};
    /** 左子节点 */
    TreeNode *left{};
    /** 右子节点 */
    TreeNode *right{};
    /** 值 */
    int value{};
    /** 是否为红色 */
    bool red = true;
public:
    /**
     * 构造函数。默认为红色
     * @param val 值
     */
    TreeNode(int val) : value(val), red(true) {}

    /**
     * 构造函数
     * @param isRed 是否为红色
     */
    TreeNode(bool isRed) : red(isRed) {}

    /**
     * 构造函数, 默认为红色
     * @param val 值
     * @param nil parent、left、right的值
     */
    TreeNode(int val, TreeNode *nil) : value(val), red(true), parent(nil), left(nil), right(nil) {}
public:
    TreeNode *getParent() const {
        return parent;
    }

    TreeNode *setParent(TreeNode *parentNode) {
        this->parent = parentNode;
        return this;
    }

    TreeNode *getLeft() const {
        return left;
    }

    TreeNode *setLeft(TreeNode *leftNode) {
        this->left = leftNode;
        return this;
    }

    TreeNode *getRight() const {
        return right;
    }

    TreeNode *setRight(TreeNode *rightNode) {
        TreeNode::right = rightNode;
        return this;
    }

    int getValue() const {
        return value;
    }

    TreeNode *setValue(int val) {
        this->value = val;
        return this;
    }

    bool isRed() const {
        return red;
    }

    TreeNode *setRed(bool isRed) {
        this->red = isRed;
        return this;
    }

    bool isBlack() const {
        return !red;
    }
};//TreeNode end

通过left、right、parent指针分别表示左子、右子和父节点
value：表示要存储的值，这里直接使用int表示，而实际可以更换为模板，然后设计hash函数
red：表示是否为红色
并提供相关的get/set函数来操作private的值

2.1.2 树容器设计

树的容器主要操作上述的TreeNode对象，主要提供的开放函数有：

插入、删除、查找
按照中序遍历查找某节点的后继节点
层序遍历、中序遍历

其中没有修改接口，实际使用模板可以提供修改接口。主要的内部函数有：

左旋、右旋
插入修复
删除修复

TreeBin类设计如下：

class TreeBin {
private:
    /** 根节点 */
    TreeNode *root;
    /** NIL节点, 默认为黑色, 其左子、右子都是自己 */
    TreeNode *nil;
private:
    /**
     * 左旋
     * @param node 当前节点
     */
    void leftRotate(TreeNode *node);

    /**
     * 右旋
     * @param node 当前节点
     */
    void rightRotate(TreeNode *node);

    /**
     * 插入时修复
     * @param node 被插入的节点
     */
    void fixInsertion(TreeNode *node);

    /**
     * 删除时修复
     * @param node 待修复的当前节点
     */
    void fixRemove(TreeNode *node);

public:
    /**
     * 构造函数
     */
    TreeBin();

    /**
     * 析构
     */
    ~TreeBin();

    /**
     * 添加数据
     * @param val 数据
     * @return true/false
     */
    bool insert(int val);

    /**
     * 删除数据
     * @param val 要删除的数据
     * @return true/false
     */
    bool remove(int val);

    /**
     * 查找数据节点
     * @param val 数据
     * @return 数据节点
     */
    TreeNode *search(int val);

    /**
     * 按照中序遍历查找指定节点的后继节点
     * @param node 指定节点
     * @return 中序后继节点
     */
    TreeNode *inOrderSuccessor(TreeNode *node);

    /**
     * 层序遍历
     */
    void printTree();

    /**
     * 中序遍历
     * @param node 节点
     */
    void printMiddle(TreeNode *node);
};//TreeBin end

构造函数主要是创建nil节点（黑色），指定左右子节点都是自己，并更新root指针：

/**
 * 构造函数
 */
TreeBin::TreeBin() {
    this->nil = new TreeNode(false);
    this->nil->setLeft(nil);
    this->nil->setRight(nil);
    this->root = this->nil;
}

2.2 左旋和右旋

在介绍插入和删除之前，我们需要先了解左旋和右旋，后面才能更好的理解插入和删除。我们以如下图为例图进行说明：
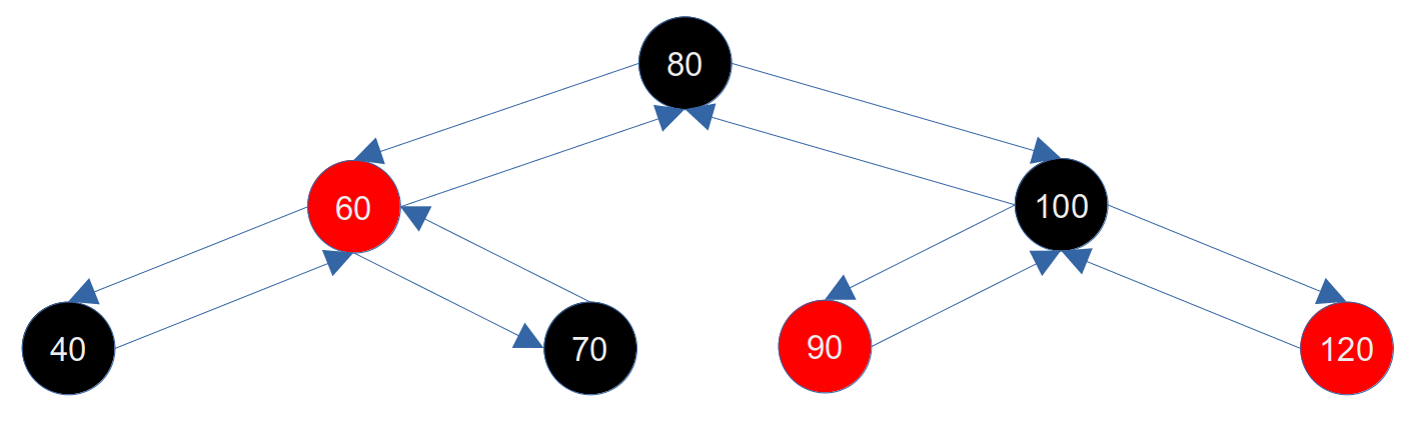
RedBlackTree-2.2-1

注意，左旋或者右旋只改变相关节点的指针，不改变节点的颜色。

2.2.1 左旋

按照80节点左旋之后的图如下所示：
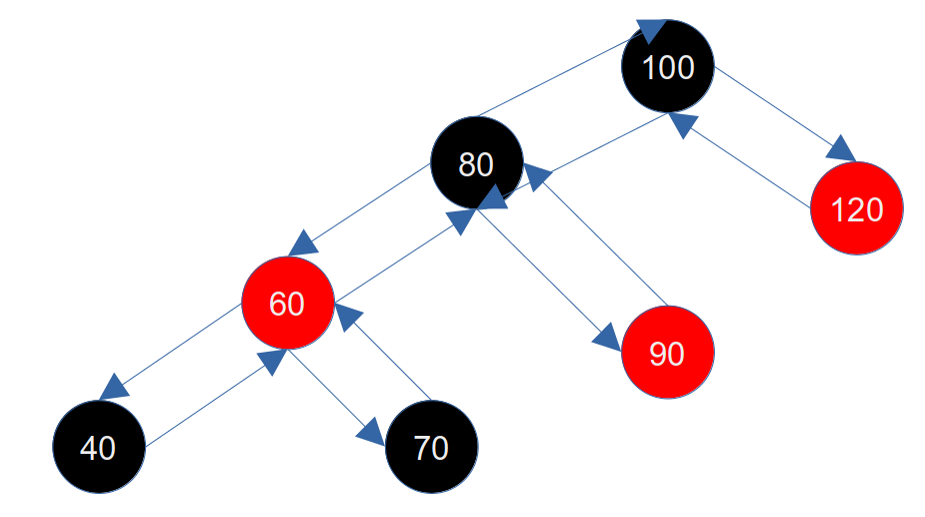
RedBlackTree-2.2.1-1

从上图可以得出：

左旋是将当前节点（80）的右子节点（100）提起，变成当前节点（80）的父节点，当前节点（80）会变成右子节点（100）的左子节点
同时会将右子节点（100）的父节点更新成当前节点（80）的父节点，此时会存在三种情况：
- 如果当前节点（80）是根节点那么新的根节点就是右子节点（100）
- 如果当前节点（80）是父节点的左子节点，那么当前节点（80）的左子节点就更新成了原右子节点（100）
- 如果当前节点（80）是父节点的右子节点，那么当前节点（80）的右子节点就更新成了原右子节点（100）
原右子节点（100）的左子节点（90）会接到当前节点（80）的右子节点上，原右子节点（100）的左子节点（90）的父节点更新成当前节点（80）

虽然很拗口，但是逻辑上其实就是一些指针的变更，主要按照当前节点（80）左旋，所以其右子节点提起成新的当前节点的父节点，然后变更相关节点的指针即可。其代码如下：

/**
 * 左旋
 * @param node 当前节点
 */
void TreeBin::leftRotate(TreeNode *node) {
    TreeNode *rightNode = node->getRight();//原右子节点
    rightNode->setParent(node->getParent());//原右子节点的父节点更新成当前节点的父节点
    node->setRight(rightNode->getLeft());//当前节点的右子节点更新成原右子节点的左子节点
    if (rightNode->getLeft() != nil) {
        rightNode->getLeft()->setParent(node);//原右子节点的父节点更新成当前节点
    }

    if (node == root) {//当前节点是根节点
        root = rightNode;//更新根节点
    } else if (node == node->getParent()->getLeft()) {//当前节点是其父节点的左子节点
        node->getParent()->setLeft(rightNode);//更新当前节点的父节点的左子节点为原右子节点
    } else {//当前节点是其父节点的右子节点
        node->getParent()->setRight(rightNode);//更新当前节点的父节点的右子节点为原右子节点
    }

    rightNode->setLeft(node);//原右子节点的左子节点更新成当前节点
    node->setParent(rightNode);//当前节点的父节点更新成原右子节点
}

2.2.2 右旋

按照80节点经过右旋之后的图如下所示：
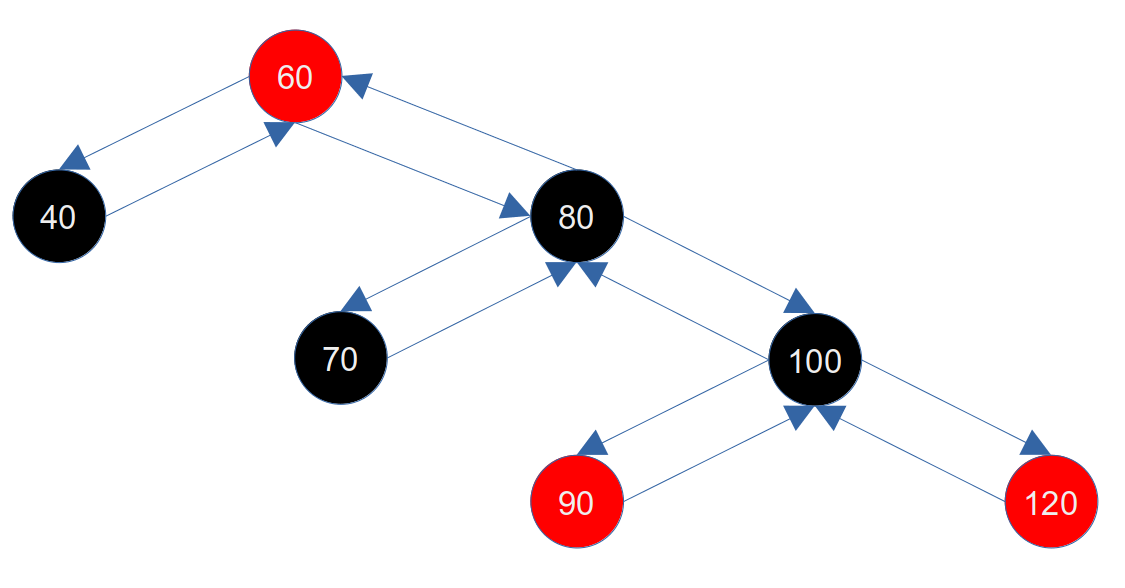
RedBlackTree-2.2.2-1

右旋与上述的左旋是相反的，不用再次进行推理，其逻辑如下：

右旋是将当前节点（80）的左子节点（60）提起，变成当前节点（80）的父节点，当前节点（80）会变成左子节点（60）的右子节点
同时会将左子节点（60）的父节点更新成当前节点（80）的父节点，此时会存在三种情况：
如果当前节点（80）是根节点那么新的根节点就是左子节点（60）
如果当前节点（80）是父节点的左子节点，那么当前节点（80）的左子节点就更新成了原左子节点（60）
如果当前节点（80）是父节点的右子节点，那么当前节点（80）的右子节点就更新成了原左子节点（60）
原左子节点（60）的右子节点（70）会接到当前节点（80）的左子节点上，原左子节点（60）的右子节点（70）的父节点更新成当前节点（80）

代码如下：

/**
 * 右旋
 * @param node 当前节点
 */
void TreeBin::rightRotate(TreeNode *node) {
    TreeNode *leftNode = node->getLeft();//原左子节点
    leftNode->setParent(node->getParent());//原左子节点的父节点更新成当前节点的父节点
    node->setLeft(leftNode->getRight());//当前节点的左子节点更新成原左子节点的右子节点
    if (leftNode->getRight() != nil) {
        leftNode->getRight()->setParent(node);//原左子节点的右子节点的父节点更新成当前节点
    }

    if (node == root) {//当前节点是根节点
        root = leftNode;//更新根节点
    } else if (node == node->getParent()->getLeft()) {//当前节点是其父节点的左子节点
        node->getParent()->setLeft(leftNode);//更新当前节点的父节点的左子节点为原左子节点
    } else {//当前节点是其父节点的右子节点
        node->getParent()->setRight(leftNode);//更新当前节点的父节点的右子节点为原左子节点
    }

    leftNode->setRight(node);//原左子节点的右子节点更新成当前节点
    node->setParent(leftNode);//当前节点的父节点更新成原左子节点
}

2.3 红黑树的插入

红黑树的插入可能会打破红黑树的上述规则，主要打破的是规则4(红节点的子节点必须是黑色)和规则5(任一节点到叶子节点的简单路径黑高度相同)，而打破规则4后的修复代价比打破规则5后的修复代价低，所以我们默认插入的节点的颜色是红色。如果是红色，那么此时只需要考虑其父节点的颜色，如果是黑色则不用修复，只有其父节点也是红色才需要修复，因为会打破规则4。所以修复的循环条件是插入节点的父节点也是红色的。插入节点的代码如下：

/**
 * 添加数据
 * @param val 数据
 * @return true/false
 */
bool TreeBin::insert(int val) {
    //先找到待插入节点的父节点 Start
    TreeNode *findNode = nil;
    TreeNode *indexNode = root;
    while (indexNode != nil) {
        findNode = indexNode;
        //已经存在节点了, 不执行插入动作 Start
        if (val == indexNode->getValue()) {
            return false;
        }
        //已经存在节点了, 不执行插入动作 End
        //在左边 Start
        if (val < indexNode->getValue()) {
            indexNode = indexNode->getLeft();
            continue;
        }
        //在左边 End

        indexNode = indexNode->getRight();//在右边
    }
    //先找到待插入节点的父节点 End

    //将数据插入到树中 Start
    TreeNode *newNode = new TreeNode(val, nil);//默认为红色
    newNode->setParent(findNode);//更新父节点
    if (findNode == nil) {//根节点
        this->root = newNode;
    } else if (val < findNode->getValue()) {//左边
        findNode->setLeft(newNode);
    } else {//右边
        findNode->setRight(newNode);
    }
    //将数据插入到树中 End

    fixInsertion(newNode);//执行修复
    return true;
}

需要先找到待插入节点的父节点，然后执行指针指向动作即可，经过上述分析，插入节点后可能会打破红黑树的平衡，所以需要经过fixInsertion(TreeNode*) 函数修复红黑树。

2.3.1 插入修复分析

怎么修复是一个需要考虑的问题。我们一步一步分析。下面的分析过程是插入节点的父节点在其祖父节点的左侧为例分析的，而父节点在祖父节点右侧与之相反即可。所以逻辑推理我们只推理一边即可。

2.3.1.1 叔父节点是红色

我们按照 1.1 红黑树定义 的图分析，插入顺序是 120、100、140，此时图就变成如下：
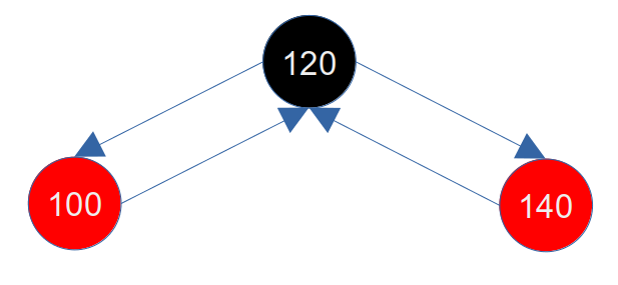
RedBlackTree-2.3.1.1-1
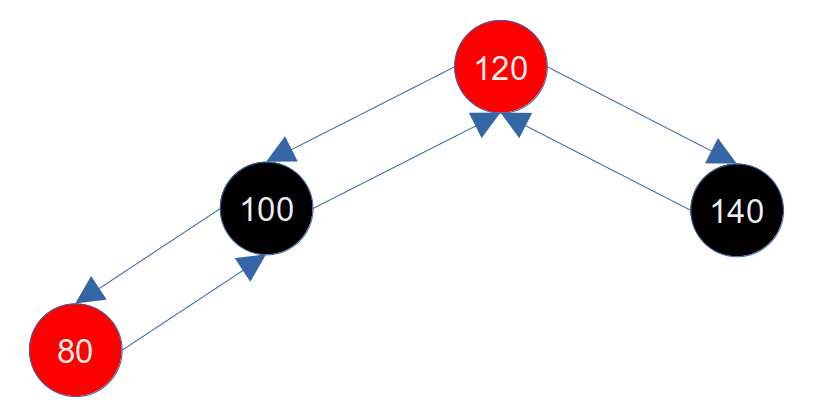
此时我们插入80，80会插入到100的左子节点上，变成如下：
RedBlackTree-2.3.1.1-2

此时打破了红黑树的规则4（两个红节点不能相连），那么可以思考怎么修复？
这种情况修复其实很简单，将叔父节点（140）染黑，将父节点（100）染黑，将祖父节点（120）染红，这样就保证了120左右两测的黑平衡。此时如下图所示：
RedBlackTree-2.3.1.1-3

如果120不是根，也不会破坏根的另一侧黑平衡。因为120被染红了，这样这一侧的黑节点没有增减，保持了黑平衡。但是此时可能会打破120之上的树平衡，所以此时将当前节点（80）更新成祖父节点（120），继续往上回溯即可。如果120是根，那么其父节点（nil是黑色）是黑色，所以会退出循环，最终我们可以在循环外将根节点染黑即可。

2.3.1.2 叔父节点是黑色

我们继续如上图所示（插入顺序是120、140、100、80），此时红黑树如下：
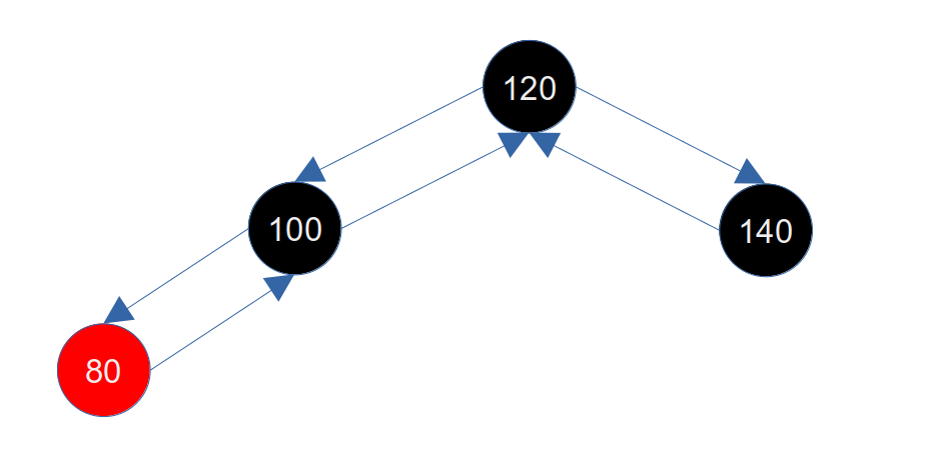
RedBlackTree-2.3.1.2-1

2.3.1.2.1 插入节点在其父节点左侧

此时我们继续插入一个60节点，节点会插入到80的左子节点上，插入后如下图所示：
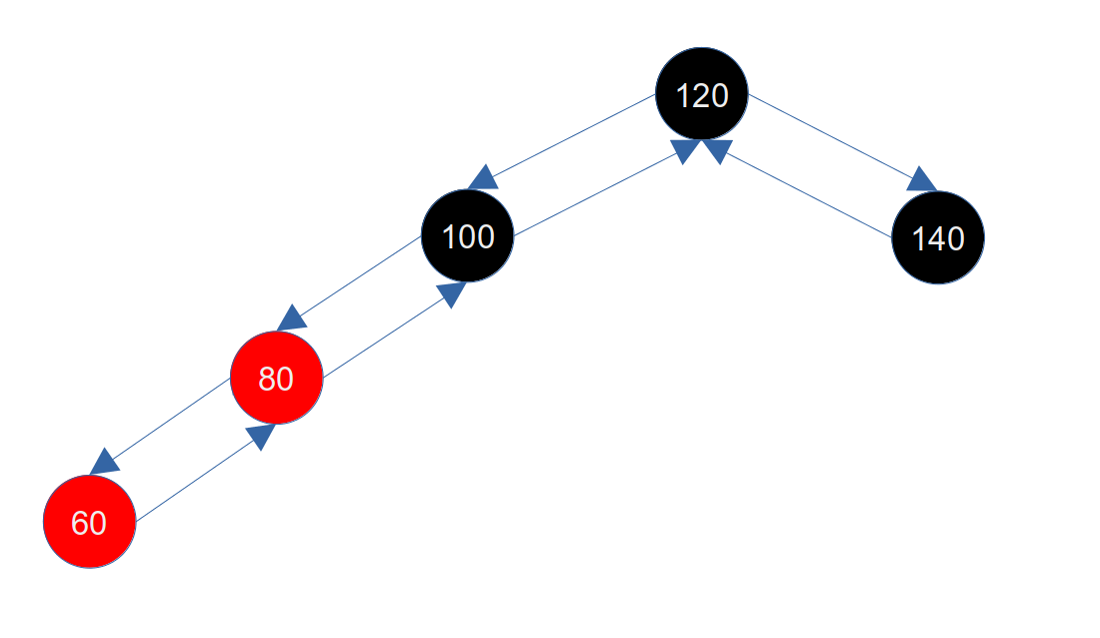
RedBlackTree-2.3.1.2.1-1

此时其叔父节点（100的右子节点）是nil，是一个黑节点。这种修复也很简单，只需要将父节点（80）染黑，并将祖父节点（100）染红，然后对祖父节点（100）右旋即可保持红黑树的平衡，如下图所示：
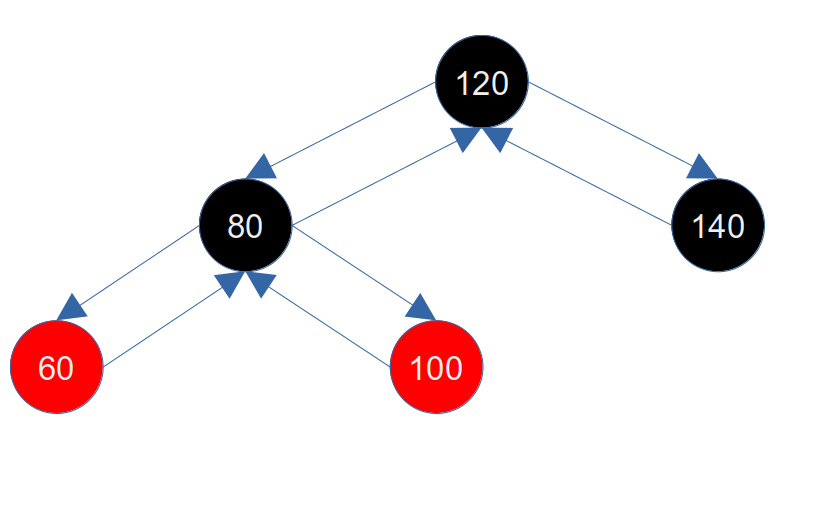
RedBlackTree-2.3.1.2.1-2

经过旋转之后，也不会打破黑平衡，同时60的父节点是黑色，退出循环，修复完成。

2.3.1.2.2 插入节点在其父节点右侧

此时我们不插入60节点，而是插入一个90节点，90节点是80节点的右子节点，如下图所示：
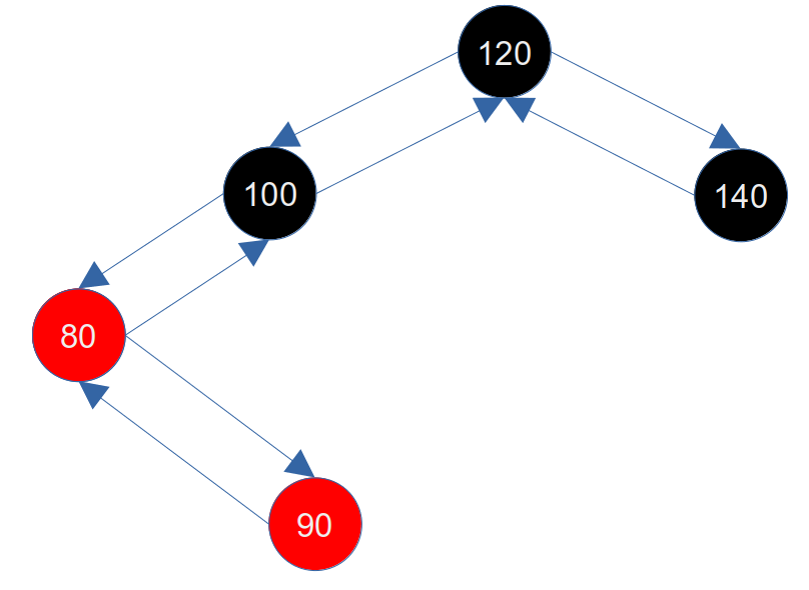
RedBlackTree-2.3.1.2.2-1

此时我们不能按照 2.3.1.2.1 插入节点在其父节点左侧 方式处理，因为如果直接右旋祖父节点（100）的话，100被染红，90接到100的左子节点上，两个红节点打破了红黑树的规则4，所以需要经过进一步处理：将当前节点更新成其父节点（80），然后左旋当前节点（80），这样90节点就变成了80节点的父节点，80变成了90节点的左子节点，100的左子节点变成了90节点，如下图所示：
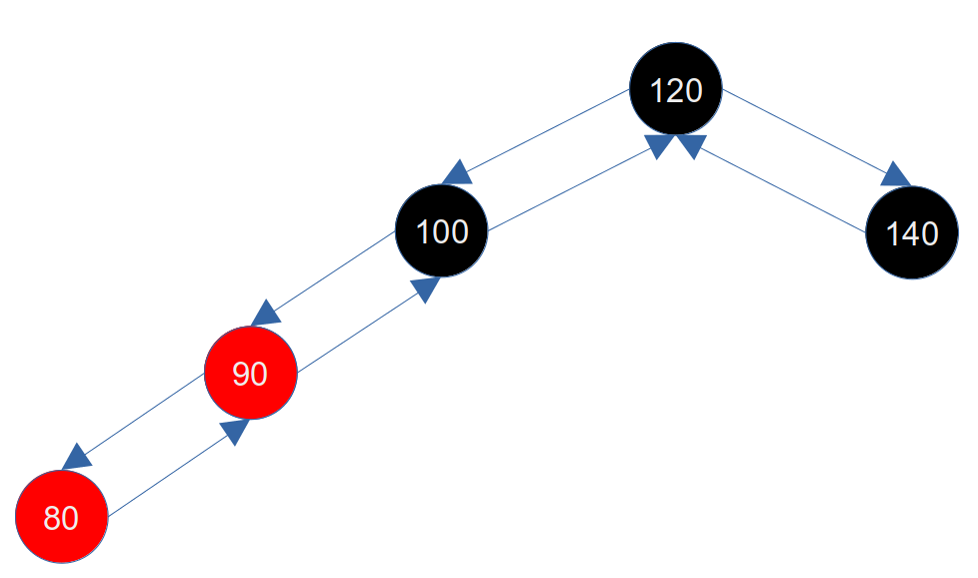
RedBlackTree-2.3.1.2.2-2

此时情况就变成了 2.3.1.2.1 插入节点在其父节点左侧 的情况，按照上述修复即可。

2.3.2 插入修复代码

经过上述的分析，其实红黑树的插入已经很清楚了，只需要将其实现即可，上述分析的是父节点在祖父节点的左侧，而右侧只需要与之相反即可。修复代码 fixInsertion(TreeNode*) 代码如下：

/**
 * 插入时修复。插入的节点默认为红色, 那么只有当其父节点为红色的时候, 会打破两个红色节点不能相连的规则, 所以需要修复。那么循环的条件
 * 就是其父节点也是红色的
 * @param node 被插入的节点
 */
void TreeBin::fixInsertion(TreeNode *node) {
    TreeNode *uncleNode;
    while (node->getParent()->isRed()) {
        //父节点在其祖父节点左边 Start
        if (node->getParent() == node->getParent()->getParent()->getLeft()) {
            uncleNode = node->getParent()->getParent()->getRight();//叔父节点
            /*
             * 修复的本质原则肯定是将父节点染黑(这样才能退出循环), 并且不打破黑高度平衡的原则。到这里我们知道父节点是红色的, 那么其祖父节点
             * 一定是黑色的(否则之前的红黑树两红相连, 破坏规则)。此时需要考虑叔父节点的颜色:
             * 1、叔父节点是红色的: 这种情况只需要将父节点和叔父节点染黑, 将祖父节点染红, 这样黑高度保持不变; 但是其祖父染红了, 就可能破坏
             * 规则4(两红不能相连), 所以将当前节点更新成其祖父节点, 继续往上回溯即可。
             * 2、叔父节点是黑色的: 此时不能按照上述方式处理, 因为会导致左侧的黑高度比右侧黑高度多一个, 所以需要通过旋转解决。所以此时需要
             * 考虑当前节点在其父节点的左边还是右边:
             *  2.1 当前节点在其父节点左边: 这种情况只需要将父节点染黑, 祖父节点染红, 然后右旋祖父节点, 这样两边的黑节点的数量都保持不变,
             *  且父节点不是红色。此时有人会考虑, 那父节点的原右子节点不是会接到祖父节点的左子节点上吗? 这种也不需要担心, 因为父节点的原右子
             *  节点一定是黑色的(父节点是红色, 那么原两个子节点一定是黑色(nil也是黑色)), 所以变更方向也不会导致黑高度失衡
             *  2.2 当前节点在其父节点右边: 此时不能按照方式 2.1 处理, 因为会打破黑高度平衡的规则(因为右旋祖父节点, 当前节点就接到了祖父
             *  节点的左子节点上, 而祖父节点的右子节点(原叔父节点)是黑色的, 这样就黑高度就不平衡了), 所以我们可以将当前节点更新成其父节点,
             *  然后左旋当前节点, 这样情况就成了 2.1 的情况了, 按照 2.1 方式处理即可
             */
            //叔父节点是红色的 Start
            if (uncleNode->isRed()) {
                node->getParent()->setRed(false);//父节点染黑
                uncleNode->setRed(false);//叔父节点染黑
                node->getParent()->getParent()->setRed(true);//祖父节点染红
                node = node->getParent()->getParent();
                continue;
            }
            //叔父节点是红色的 End

            //叔父节点是黑色的 Start
            if (node == node->getParent()->getRight()) {//当前节点在其父节点的右边
                node = node->getParent();
                leftRotate(node);//左旋
            }
            node->getParent()->setRed(false);//父节点染黑
            node->getParent()->getParent()->setRed(true);//祖父节点染红
            rightRotate(node->getParent()->getParent());//右旋祖父节点
            //叔父节点是黑色的 End
            continue;
        }
        //父节点在其祖父节点左边 End

        //父节点在其祖父节点右边(无需再次推理, 与上述相反) Start
        uncleNode = node->getParent()->getParent()->getLeft();//叔父节点
        //叔父节点是红色的 Start
        if (uncleNode->isRed()) {
            node->getParent()->setRed(false);//父节点染黑
            uncleNode->setRed(false);//叔父节点染黑
            node->getParent()->getParent()->setRed(true);//祖父节点染红
            node = node->getParent()->getParent();
            continue;
        }
        //叔父节点是红色的 End

        //叔父节点是黑色的 Start
        if (node == node->getParent()->getLeft()) {//当前节点在其父节点的左边
            node = node->getParent();
            rightRotate(node);//左旋
        }
        node->getParent()->setRed(false);//父节点染黑
        node->getParent()->getParent()->setRed(true);//祖父节点染红
        leftRotate(node->getParent()->getParent());//左旋祖父节点
        //叔父节点是黑色的 End
        //父节点在其祖父节点右边(无需再次推理, 与上述相反) End
    }

    this->root->setRed(false);//上述循环可能回溯到根, 那么将根染黑
}

2.4 红黑树查找

红黑树的查找其实很简单，查找的节点从根开始，如果给定的值比查找的节点的值小，那么证明要找的节点在查找的节点的左边，否则就在右边。从这里可以看出红黑树的查找时间复杂度是O(logN)的，其中底数是2。这种树状的数据结构，如果是二叉树，底数都是2，如果是2-3树，底数是3，如果是2-3-4树，底数就是4，以此类推。但是其实这个底数并没有太多的意义，因为当N的值越大，结果值之间的差值对于CPU的运算速度来说几乎可以忽略不计，所以一般不会细究其底数的问题（N值越小更可以忽略了）。search(int) 代码如下：

/**
 * 查找数据节点
 * @param val 数据
 * @return 数据节点
 */
TreeNode *TreeBin::search(int val) {
    TreeNode *findNode = root;
    while (findNode != nil) {
        //找到了 Start
        if (val == findNode->getValue()) {
            break;
        }
        //找到了 End

        //在左边 Start
        if (val < findNode->getValue()) {
            findNode = findNode->getLeft();
            continue;
        }
        //在左边 End

        findNode = findNode->getRight();//在右边
    }

    return findNode != nil ? findNode : nullptr;
}

2.5 按照中序遍历查找后继节点

中序遍历表示以根为原点，先遍历左子树，再遍历右子树，以 1.1 红黑树定义 中展示的红黑树来说，中序遍历的结果是：10、20、40、60、65、80、90、100、101、110、115、120、140、160。我们可以找一下二叉树的中序后继的规律：

如果某个节点存在右子节点，那么后继节点一定在右子节点上，并且是在右子节点的最左子孙节点上。比如根节点100，它下一个遍历的节点是右子节点的最左孙子节点101
如果某个节点不存在右子节点，那么需要找出对应的节点是在其父节点的左子还是右子：
- 如果是在其父节点的左子节点，那么下一个遍历的就是其父节点，后继节点也就是父节点
- 如果在其父节点的右子节点，那么就需要一直往上找，直到找到节点在其父节点的左侧为止，此时就变成了上述的情况。比如65节点，它的后继节点是80

经过上述分析，代码的逻辑就很清晰了，inOrderSuccessor(TreeNode)* 代码如下：

/**
 * 按照中序遍历查找指定节点的后继节点
 * @param node 指定节点
 * @return 中序后继节点
 */
TreeNode *TreeBin::inOrderSuccessor(TreeNode *node) {
    //存在右子节点 Start
    TreeNode *findNode;
    if (node->getRight() != nil) {
        findNode = node->getRight();
        while (findNode->getLeft() != nil) {//一直往左找
            findNode = findNode->getLeft();
        }
        return findNode;
    }
    //存在右子节点 End

    //不存在右子节点 Start
    findNode = node;
    while (findNode != root && findNode != findNode->getParent()->getLeft()) {
        findNode = findNode->getParent();
    }
    return findNode->getParent();
    //不存在右子节点 End
}

2.6 红黑树的删除

红黑树的删除要比添加操作还要复杂。删除操作首先找到值对应的节点，然后可以分为两种情况：

找到的节点既有左子节点也有右子节点：这种情况可以找到其后继节点，不管是中序后继还是前序后继（本文使用的是中序后继），然后真正删除的是后继节点，将找到的节点的数据（value）替换成后继节点的数据（value）。而后继节点的右子节点会接到删除节点的父节点的右子节点上，所以真正删除的是后继节点
找到的节点只有左子或者右子或者没有子节点：这种情况被删除的节点就是找到的节点，其子节点接到其父节点上即可

找到了待删除节点后，更新相关的指针。如果删除的节点是红色的，那么不需要任何操作；但是如果删除的节点是黑色的，就需要修复了，因为一定会破坏规则5（黑高度平衡）。注意，这里修复是从待删除的节点的子节点开始，因为待删除的节点此时已经从树中去除了。
remove(int) 代码如下：

/**
 * 删除数据
 * @param val 要删除的数据
 * @return true/false
 */
bool TreeBin::remove(int val) {
    //先找到对应的节点 Start
    TreeNode *findNode = search(val);
    if (findNode == nullptr) {//树中没有对应的数据
        return false;
    }
    //先找到对应的节点 End

    TreeNode *deleteNode, *deleteNodeSon;//真正删除节点及其子节点
    if (findNode->getLeft() != nil && findNode->getRight() != nil) {//存在左子和右子节点
        deleteNode = inOrderSuccessor(findNode);//找到后继节点
        deleteNodeSon = deleteNode->getRight();//可以确定其子节点是右子节点(nil节点也算)
    } else {
        deleteNode = findNode;//找到的节点就是删除的节点
        if (deleteNode->getLeft() != nil) {//左子存在
            deleteNodeSon = deleteNode->getLeft();
        } else {//右子存在(nil也算)
            deleteNodeSon = deleteNode->getRight();
        }
    }

    findNode->setValue(deleteNode->getValue());//将真正删除节点的数据替换
    deleteNodeSon->setParent(deleteNode->getParent());//将子节点的父节点更新成其祖父节点
    if (deleteNode == root) {//删除的是根节点
        root = deleteNodeSon;//更新根的指针
    } else if (deleteNode == deleteNode->getParent()->getLeft()) {//删除节点在其父节点左边
        deleteNode->getParent()->setLeft(deleteNodeSon);
    } else {//删除节点在其父节点右边
        deleteNode->getParent()->setRight(deleteNodeSon);
    }

    //黑色才需要修复 Start
    if (deleteNode->isBlack()) {
        fixRemove(deleteNodeSon);//修复
    }
    //黑色才需要修复 End
    delete deleteNode;//回收内存

    return true;
}

2.7 删除修复

红黑树最复杂的地方就是在删除后的修复了。上述已经介绍了删除的逻辑，而修复是从被删除的节点的子节点开始（下文称当前节点）。因为被删除的节点是黑色的，所以修复的宗旨就是将这个黑色节点增加回来才能保证红黑树的整体平衡，而怎么增加黑色节点是修复的关键，如果当前节点是红色的，那么直接将其染黑就可以让红黑树黑高度重新平衡；如果当前节点是黑色的，那么就需要进行修复，所以修复的循环应当是当前节点是黑色的并且不为根（根节点不需要修复）。我们以一侧为例，另一侧与之相反即可。下文的分析逻辑是以当前节点在其父节点的右侧为例。
那么最终怎么让红黑树保持黑高度平衡是一个关键的地方，因为右侧被删除了一个节点，所以肯定是需要通过旋转的方式将这个节点增加回来，而旋转之后需要保持红黑树的平衡，所以此时我们需要看兄弟节点的颜色情况以及兄弟节点的子节点颜色情况才能分析出怎么旋转染色从而让红黑树重新平衡。此时我们可以将问题分类：

兄弟节点是黑色的
a. 兄弟节点的两个子节点是黑色的
b.兄弟节点的左子是红色右子是黑色
c.兄弟节点的左子是黑色右子是红色
d.兄弟节点的两个子节点是红色的
兄弟节点是红色的

2.7.1 兄弟节点是黑色

我们以 1.1 红黑树定义 中的图为例，以根的右侧图为例进行说明，如下图：
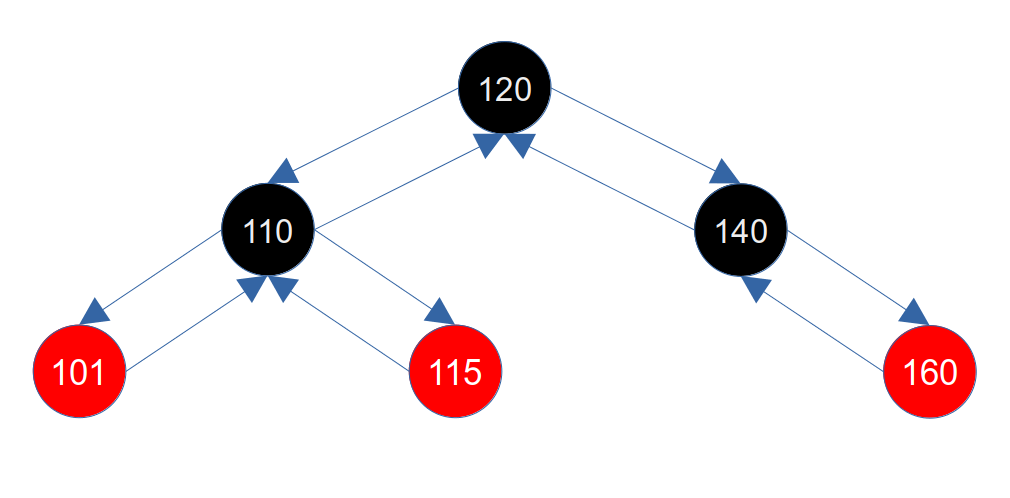
RedBlackTree-2.7.1-1
此时我们先删除160节点，因为160节点是红色节点，所以不需要修复，不影响红黑树的平衡，删除后的图如下：
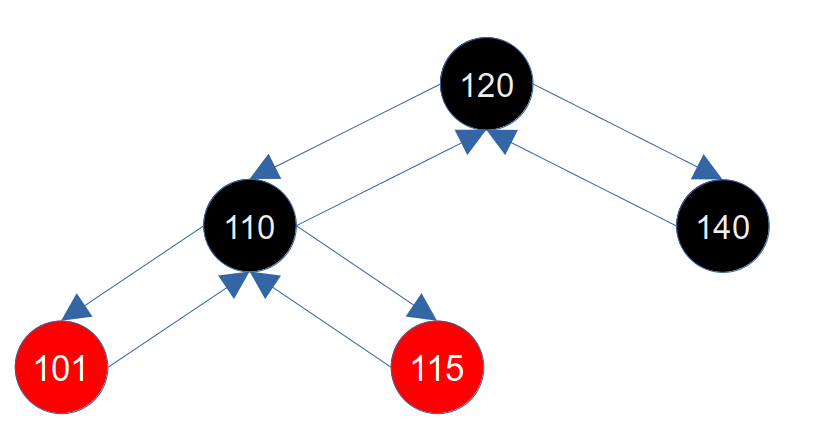
RedBlackTree-2.7.1-2

2.7.1.1 兄弟节点的两个子节点是黑色

这里我们先删除101和115节点，这两个节点都是红色的，所以不影响红黑树的平衡，删除后如下图所示：
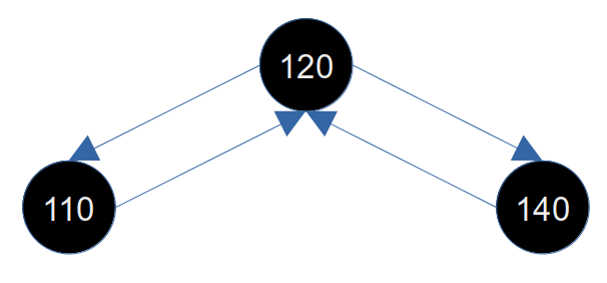
RedBlackTree-2.7.1.1-1

接下来我们删除140节点，那么其右子节点是一个nil节点，也是黑色的，所以需要进行修复。而兄弟节点（110）是黑色的，并且兄弟节点的两个子节点也是黑色的（nil），符合当前这种情况。删除后的图如下所示：
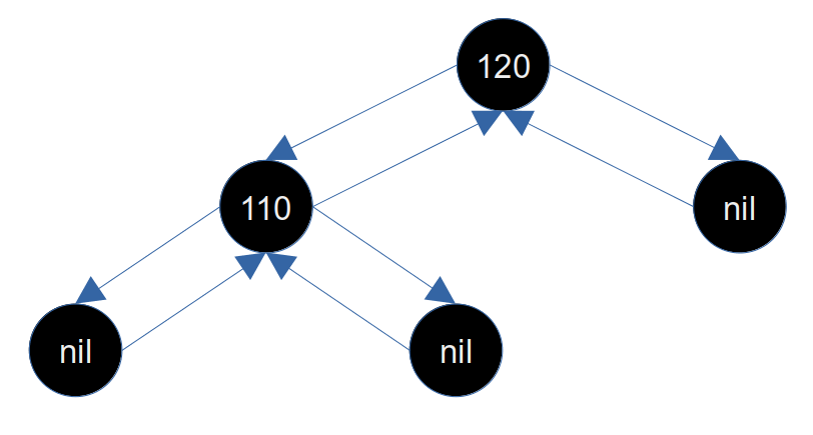
RedBlackTree-2.7.1.1-2

上图我们将叶子节点也加上了，方便分析。此时兄弟节点（110）侧比当前节点侧多一个黑色节点，那么我们可以直接将兄弟节点（110）染成红色，这样兄弟节点（110）侧就会减少一个黑节点，这样局部的黑高度就平衡了，如下图所示：
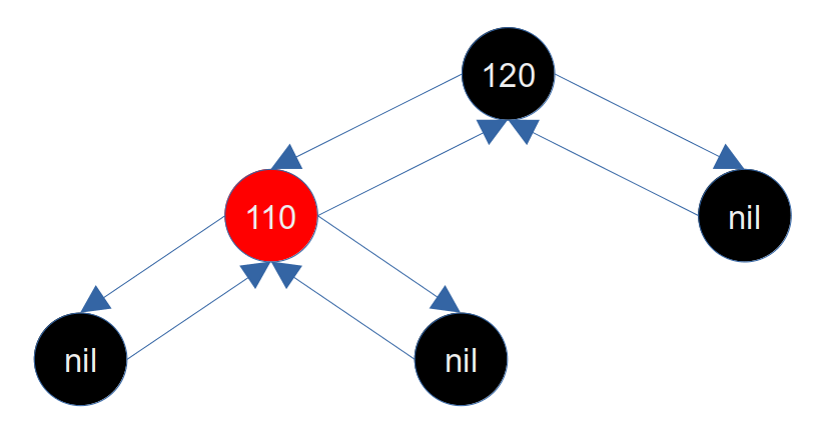
RedBlackTree-2.7.1.1-3

但是这种解决方式还没有将被删除的黑色节点增加回来，红黑树整体还是没有达到黑高度平衡（根的另一侧还是多一个黑节点），所以我们需要将当前节点更新成其父节点（120），继续往上回溯修复。那么此时存在两种情况：

如果父节点（120）是红色的，那么就会退出循环后将120染黑，这样左右两侧都增加了一个黑节点，没有破坏黑高度平衡。同时增加了一个黑节点，与根的另一侧保持了黑高度平衡
如果父节点（120）是黑色的，那么在循环中就会继续修复。

所以修复兄弟节点是黑节点，并且兄弟节点的两个子节点也是黑节点这种情况的方式就是：

将兄弟节点染红
将当前节点更新成其父节点继续循环修复

2.7.1.2 兄弟节点的左子是红色右子是黑色

此时我们将115节点删除（2.7.1中的图），115是红色，所以不影响红黑树的平衡，删除后如下图所示：
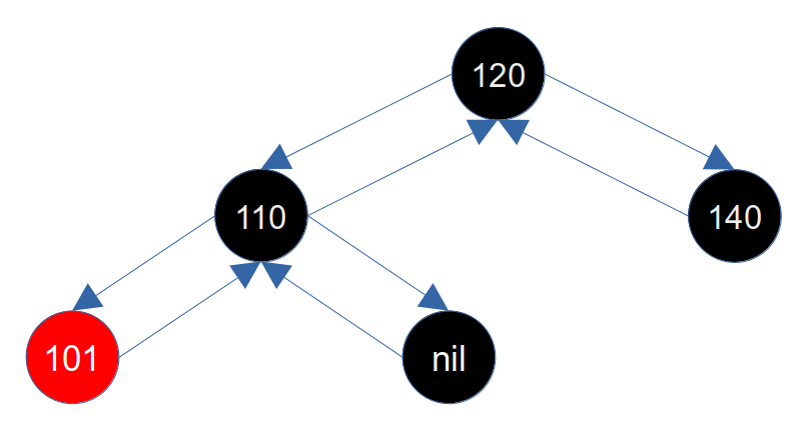
RedBlackTree-2.7.1.2-1
这时候我们再删除140，此时兄弟节点（110）是红色，兄弟节点是左红右黑的情况，符合当前场景，删除140后如下图所示：
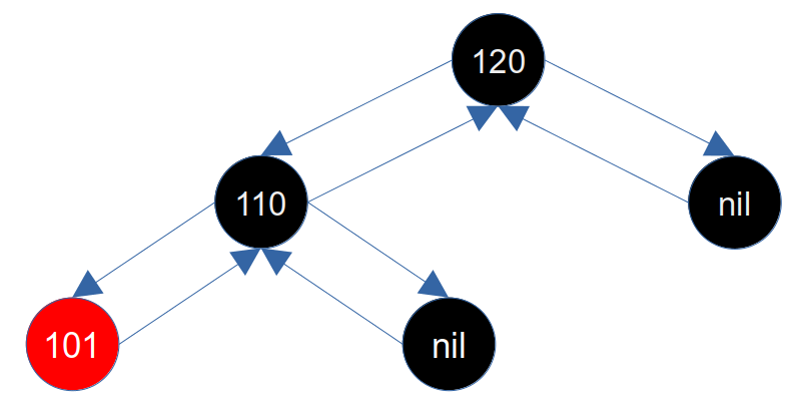
RedBlackTree-2.7.1.2-2
这种情况下，其实也很简单，只需要将兄弟节点（110）的左子节点染黑，将兄弟节点（110）染成其父节点（120）的颜色，然后将父节点（120）染黑，最后右旋父节点（120）就保证了红黑树的平衡。如下图所示：
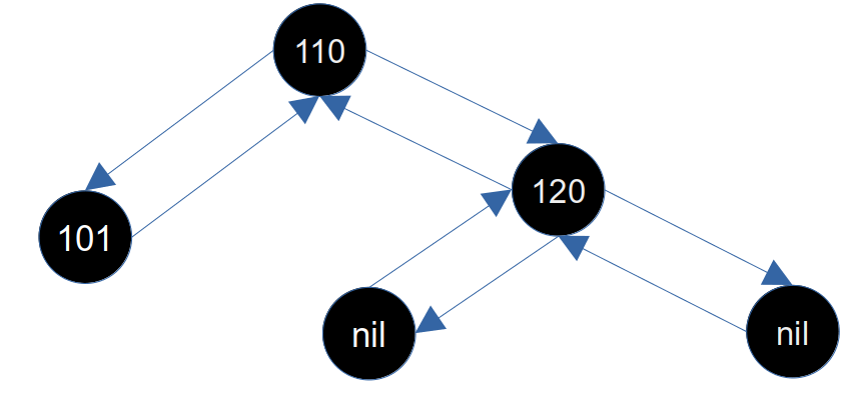
RedBlackTree-2.7.1.2-3

原兄弟节点（110）的右子（黑色）会接到父节点（120）的左子节点上，这样父节点（120）的左子和右子都是黑色，这部分保持了平衡；同时原兄弟节点（110）的左子节点（101）被染黑，父节点（120）被染黑，原兄弟节点（110）颜色与父节点颜色相同，所以现在的祖父节点（110）的左子和右子保持了平衡，父节点（120）被染黑，所以被删除的黑节点增加了回来，这样红黑树保持了整体的平衡。
所以对于这种情况：兄弟节点是黑色，并且兄弟节点的左子节点是红色，右子节点是黑色的修复逻辑是：

将兄弟节点染成其父节点的颜色
将兄弟节点的左子节点和父节点染成黑色
右旋父节点

2.7.1.3 兄弟节点的左子是黑色右子是红色

我们将101节点删除（2.7.1中的图），101是红色，所以不影响平衡，删除后如下图所示：
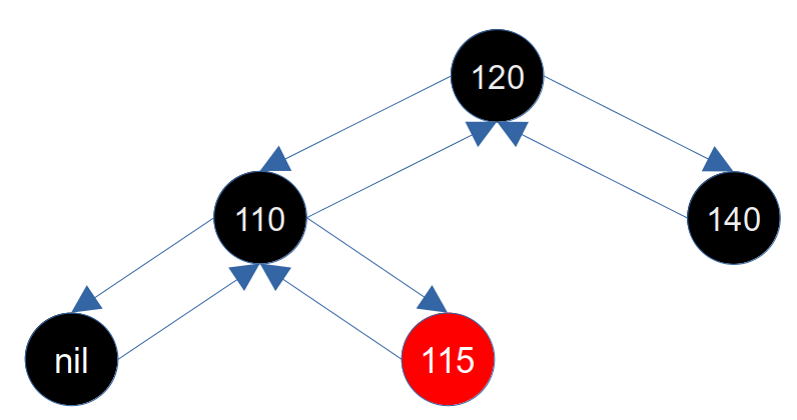
RedBlackTree-2.7.1.3-1
此时我们删除140。对于这种情况的修复，我们不能直接按照 2.7.1.2 兄弟节点的左子是红色右子是黑色 的情况修复，因为右旋父节点（120）后115节点会接到父节点（120）的左子上，此时父节点（120）的左子和右子就不平衡了。所以对于这种情况，我们可以将兄弟节点（110）染红，将兄弟节点的右子节点（115）染黑，然后左旋兄弟节点（110），这样新的兄弟节点（115）就是左红右黑的情况，如下图所示：
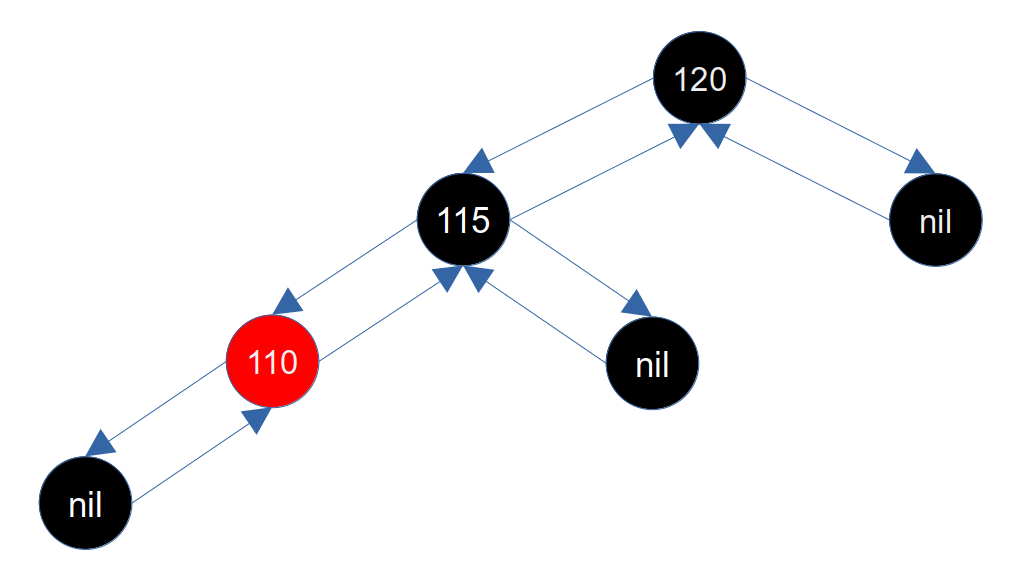
RedBlackTree-2.7.1.3-2
现在新的兄弟节点（115）就成了左红右黑的情况，修复逻辑按照 2.7.1.2 兄弟节点的左子是红色右子是黑色 修复即可。最终修复后如下图所示：
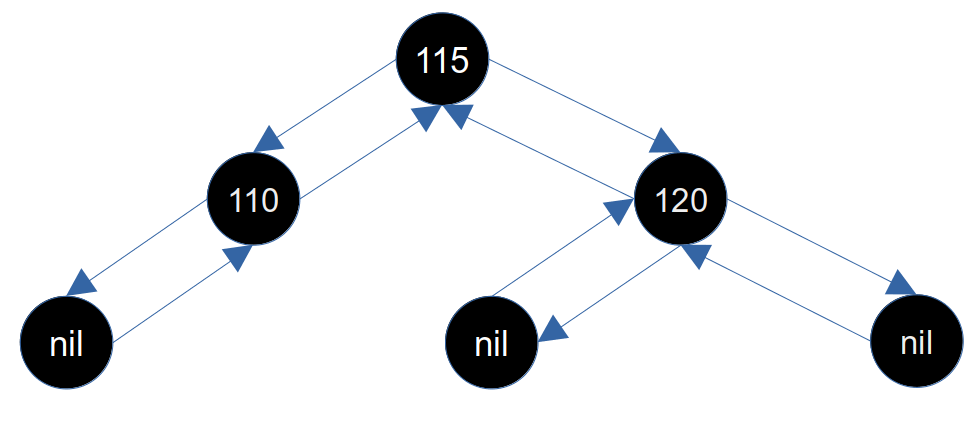
RedBlackTree-2.7.1.3-3

2.7.1.4 兄弟节点的两个子节点是红色

这种情况与 2.7.1.2 兄弟节点的左子是红色右子是黑色 其实是一样的，因为两个子节点都是红色的情况，那么按照红黑树的规则，兄弟节点的左右孙子节点一定是黑色的（黑高度以及两红不能直连），所以按照 2.7.1.2 兄弟节点的左子是红色右子是黑色 处理之后右侧会增加一个黑节点，左侧黑节点保持不变，并且右红也存在一个黑节点，所以父节点的两侧是平衡，从而达到了红黑树的整体平衡。

2.7.2 兄弟节点是红色

兄弟节点是红色的，我们现在看根左侧（1.1 红黑树定义 中的图），如下图所示：
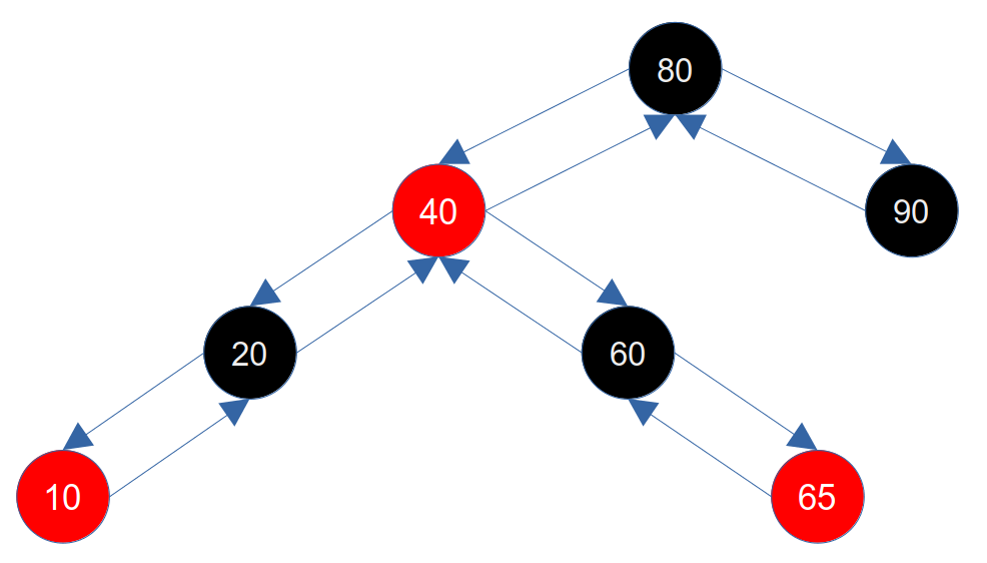
RedBlackTree-2.7.2-1
此时我们删除节点90，那么其右子节点（nil）是黑色，兄弟节点（40）是红色，符合当前情况，删除90节点后如下图所示：
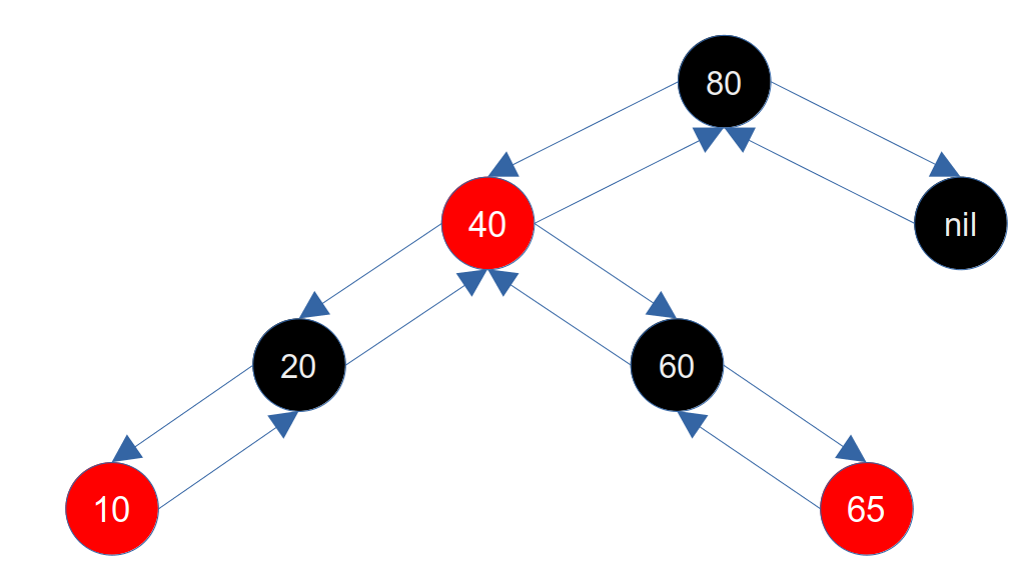
RedBlackTree-2.7.2-2
我们可以将这种情况通过旋转着色（不破坏平衡的情况下）变成 2.7.1 兄弟节点是黑色 的情况。在不破坏当前平衡的情况下，可以将兄弟节点（40）染黑，将父节点（80）染红，然后右旋父节点（80），如下图所示：
RedBlackTree-2.7.2-3

因为原兄弟节点（40）是红色，所以其左子（20）和右子（60）一定是黑色，经过旋转之后，父节点（80）两侧黑高度不变，而父节点（80）原先一定是黑色的（因为兄弟节点（40）是红色的），所以旋转之后祖父节点（40）的左右两侧情况保持不变。此时新的兄弟节点（60）就是黑色的了，最后按照 2.7.1 兄弟节点是黑色 的逻辑修复即可。

2.7.3 删除修复代码

经过上述分析，编写代码就很简单了，fixRemove(TreeNode*) 代码如下：

/**
 * 删除时修复, 被删除的节点是黑色需要修复, 此时被删除的子节点(node, 这里称当前节点)如果是红色, 那么直接将其染黑, 这样红黑树的黑高度保持了
 * 平衡, 所以这里循环的条件是当前节点是黑色的并且不是根
 * @param node 待修复的当前节点
 */
void TreeBin::fixRemove(TreeNode *node) {
    TreeNode *brotherNode;//兄弟节点
    while (node != root && node->isBlack()) {
        //当前节点在其父节点的右侧 Start
        if (node == node->getParent()->getRight()) {
            brotherNode = node->getParent()->getLeft();//兄弟节点
            /*
             * 需要将被删除的黑节点增加回来, 那么必定需要通过旋转染色的方式, 此时需要考虑兄弟节点的颜色(这里我们将nil节点也算)
             * 1、兄弟节点是黑色的: 兄弟节点是黑色的, 那么其子节点的染色是不确定的, 所以需要进一步考虑其子节点的情况:
             *  1.1 两个子节点都是黑色的: 这种情况其实很简单, 只需要将兄弟节点染红, 这样兄弟节点的两侧不会黑高度失衡, 然后将当前节点
             *  更新成其父节点, 如果父节点是红色, 那么退出循环后会将当前节点染黑, 这样红黑树的整体就达到了黑高度平衡(被删除的黑色增加了);
             *  如果父节点是黑色, 那么循环继续修复即可
             *  1.2 左子是红色右子是黑色: 这种情况可以将左子染黑, 将兄弟节点染成其父节点的颜色, 将父节点染黑, 然后右旋父节点, 这样原兄弟节点
             *  成了祖父节点, 父节点成了原兄弟节点的右子节点, 并且原兄弟节点的右子节点(黑色)接到了父节点的左子节点上。因为将父节点染黑, 所以
             *  黑色增加了回来, 又因为原兄弟节点的右子节点是黑色, 所以当前节点的父节点的两侧的黑高度是平衡的, 而原兄弟的左子染成了黑色, 所以原
             *  兄弟节点(当前节点的祖父节点)的两侧也保持了黑高度平衡, 红黑树达到了整体的平衡
             *  1.3 左子是黑色右子是红色: 此时不能像 1.2 情况一样处理, 因为右红会接到父节点的左子上, 这样父节点的两侧就不平衡了。所以我们先
             *  将兄弟节点染红, 将兄弟节点的右子染黑, 然后左旋兄弟节点, 这样原兄弟节点的右子(染成黑色的了)就成了新的兄弟节点, 原兄弟节点(现在是红色)
             *  就成了新的兄弟节点的左子节点, 这样就变成了左红右黑(原兄弟节点的右子是红色, 那么其子节点一定是黑色)的情况, 按照 1.2 情况处理即可
             *  1.4 左子和右子都是红色: 这种可以直接按照 1.2 情况处理, 因为按照红黑树的规则, 那么其子孙节点一定是黑色的, 所以按照 1.2 情况处理
             *  可以保持红黑树的平衡
             * 2、兄弟节点是红色的: 兄弟节点是红色, 那么父节点一定是黑色, 其两个子节点(nil也算)一定是黑色, 所以我们可以将父节点染红, 兄弟节点染黑,
             * 然后右旋父节点, 这样原兄弟节点的右子节点(黑色)会接到父节点的左子节点上, 而原兄弟节点成了祖父节点, 并且两侧黑高度不会失衡。此时
             * 新的兄弟是黑色的, 按照情况 1 处理即可。
             */
            //兄弟节点是红色的 Start
            if (brotherNode->isRed()) {
                brotherNode->setRed(false);//兄弟节点染黑
                brotherNode->getParent()->setRed(true);//父节点染红
                rightRotate(node->getParent());//右旋父节点
                brotherNode = node->getParent()->getLeft();//更新兄弟节点
            }
            //兄弟节点是红色的 End

            //兄弟节点是黑色的 Start
            //兄弟节点的两个子节点都是黑色的 Start
            if (brotherNode->getLeft()->isBlack() && brotherNode->getRight()->isBlack()) {
                brotherNode->setRed(true);//将兄弟节点染红
                node = node->getParent();//更新当前节点
                continue;
            }
            //兄弟节点的两个子节点都是黑色的 End

            //兄弟节点两个子节点颜色不同都都是红色 Start
            //兄弟节点的两个子节点是左黑右红的情况 Start
            if (brotherNode->getLeft()->isBlack()) {
                brotherNode->setRed(true);//兄弟节点染红
                brotherNode->getRight()->setRed(false);//右子染黑
                leftRotate(brotherNode);//左旋兄弟节点
                brotherNode = node->getParent()->getLeft();//更新兄弟节点
            }
            //兄弟节点的两个子节点是左黑右红的情况 End

            brotherNode->setRed(brotherNode->getParent()->isRed());//兄弟节点染成其父节点颜色
            brotherNode->getLeft()->setRed(false);//左子染黑
            brotherNode->getParent()->setRed(false);//父节点染黑
            rightRotate(node->getParent());//右旋父节点
            node = root;//退出循环
            //兄弟节点两个子节点颜色不同都都是红色 End
            //兄弟节点是黑色的 End

            continue;
        }
        //当前节点在其父节点的右侧 End

        //当前节点在其父节点的左侧(不用再次推理, 与上述相反) Start
        brotherNode = node->getParent()->getRight();//兄弟节点
        //兄弟节点是红色的 Start
        if (brotherNode->isRed()) {
            brotherNode->setRed(false);//兄弟节点染黑
            brotherNode->getParent()->setRed(true);//父节点染红
            leftRotate(node->getParent());//左旋父节点
            brotherNode = node->getParent()->getRight();//更新兄弟节点
        }
        //兄弟节点是红色的 End

        //兄弟节点是黑色的 Start
        //兄弟节点的两个子节点都是黑色的 Start
        if (brotherNode->getLeft()->isBlack() && brotherNode->getRight()->isBlack()) {
            brotherNode->setRed(true);//将兄弟节点染红
            node = node->getParent();//更新当前节点
            continue;
        }
        //兄弟节点的两个子节点都是黑色的 End

        //兄弟节点两个子节点颜色不同都都是红色 Start
        //兄弟节点的两个子节点是左红右黑的情况 Start
        if (brotherNode->getRight()->isBlack()) {
            brotherNode->setRed(true);//兄弟节点染红
            brotherNode->getLeft()->setRed(false);//左染黑
            rightRotate(brotherNode);//右旋兄弟节点
            brotherNode = node->getParent()->getRight();//更新兄弟节点
        }
        //兄弟节点的两个子节点是左红右黑的情况 End

        brotherNode->setRed(brotherNode->getParent()->isRed());//兄弟节点染成其父节点颜色
        brotherNode->getRight()->setRed(false);//右子染黑
        brotherNode->getParent()->setRed(false);//父节点染黑
        leftRotate(node->getParent());//左旋父节点
        node = root;//退出循环
        //兄弟节点两个子节点颜色不同都都是红色 End
        //兄弟节点是黑色的 End
        //当前节点在其父节点的左侧(不用再次推理, 与上述相反) End
    }
    node->setRed(false);//当前节点染黑
}

2.8 层序遍历和中序遍历

2.8.1 层序遍历

层序遍历表示从根节点开始，一层一层的遍历往下遍历，printTree() 代码如下：

/**
 * 层序遍历
 */
void TreeBin::printTree() {
    if (root == nil) {
        return;
    }

    deque<TreeNode*> nodeQueue;
    nodeQueue.push_back(root);
    int i, size;
    TreeNode *printNode, *parentPrintNode;
    while (!nodeQueue.empty()) {
        size = nodeQueue.size();
        for (i = 0; i < size; i++) {
            printNode = nodeQueue.front();
            parentPrintNode = printNode->getParent();
            nodeQueue.pop_front();
            if (printNode->getLeft() != nil) {
                nodeQueue.push_back(printNode->getLeft());
            }
            if (printNode->getRight() != nil) {
                nodeQueue.push_back(printNode->getRight());
            }

            string color = printNode->isRed() ? "RED: " : "BLACK: ";
            string val = to_string(printNode->getValue());
            string parentVal = parentPrintNode != nil ? to_string(parentPrintNode->getValue()) : "";
            string dir = parentPrintNode != nil ? (printNode == parentPrintNode->getLeft() ? "LEFT " : "RIGHT ") : "";
            cout << dir << color << val << ", PARENT: " << parentVal << "  ";
        }
        cout << endl;
    }
}

2.8.2 中序遍历

中序遍历表示先遍历左子节点, 然后遍历右子节点, printMiddle(TreeNode*) 代码如下：

/**
 * 中序遍历
 * @param node 节点
 */
void TreeBin::printMiddle(TreeNode *node) {
    if (node == nil) {
        return;
    }
    printMiddle(node->getLeft());

    string color = node->isRed() ? "RED: " : "BLACK: ";
    string val = to_string(node->getValue());
    string parentVal = node->getParent() != nil ? to_string(node->getParent()->getValue()) : "";
    string dir = node->getParent() != nil ? (node == node->getParent()->getLeft() ? "LEFT " : "RIGHT ") : "";
    cout << dir << color << val << ", PARENT: " << parentVal << "  ";

    printMiddle(node->getRight());
}

目录CONTENT

1、红黑树的原理及实现(C++)

一红黑树的原理

1.1 红黑树定义

1.2 红黑树的优点

1.3 红黑树的应用

二红黑树的实现

2.1 红黑树代码框架

2.1.1 节点设计

2.1.2 树容器设计

2.2 左旋和右旋

2.2.1 左旋

2.2.2 右旋

2.3 红黑树的插入

2.3.1 插入修复分析

2.3.1.1 叔父节点是红色

2.3.1.2 叔父节点是黑色

2.3.1.2.1 插入节点在其父节点左侧

2.3.1.2.2 插入节点在其父节点右侧

2.3.2 插入修复代码

2.4 红黑树查找

2.5 按照中序遍历查找后继节点

2.6 红黑树的删除

2.7 删除修复

2.7.1 兄弟节点是黑色

2.7.1.1 兄弟节点的两个子节点是黑色

2.7.1.2 兄弟节点的左子是红色右子是黑色

2.7.1.3 兄弟节点的左子是黑色右子是红色

2.7.1.4 兄弟节点的两个子节点是红色

2.7.2 兄弟节点是红色

2.7.3 删除修复代码

2.8 层序遍历和中序遍历

2.8.1 层序遍历

2.8.2 中序遍历

评论区

1、红黑树的原理及实现(C++)

一 红黑树的原理

1.1 红黑树定义

1.2 红黑树的优点

1.3 红黑树的应用

二 红黑树的实现

2.1 红黑树代码框架

2.1.1 节点设计

2.1.2 树容器设计

2.2 左旋和右旋

2.2.1 左旋

2.2.2 右旋

2.3 红黑树的插入

2.3.1 插入修复分析

2.3.1.1 叔父节点是红色

2.3.1.2 叔父节点是黑色

2.3.1.2.1 插入节点在其父节点左侧

2.3.1.2.2 插入节点在其父节点右侧

2.3.2 插入修复代码

2.4 红黑树查找

2.5 按照中序遍历查找后继节点

2.6 红黑树的删除

2.7 删除修复

2.7.1 兄弟节点是黑色

2.7.1.1 兄弟节点的两个子节点是黑色

2.7.1.2 兄弟节点的左子是红色右子是黑色

2.7.1.3 兄弟节点的左子是黑色右子是红色

2.7.1.4 兄弟节点的两个子节点是红色

2.7.2 兄弟节点是红色

2.7.3 删除修复代码

2.8 层序遍历和中序遍历

2.8.1 层序遍历

2.8.2 中序遍历

评论区

一红黑树的原理

二红黑树的实现